Rund um die Schule
Forum :: Notenstand :: Klassen :: Kontakt :: Private Seite
Du bist hier » Home » Mathematik » 5. Klasse » Aussagen - Mengen - Verknüpfungen
Für die richtige Darstellung der Inhalte muss JavaScript aktiviert sein!
Was sind Aussagen?
Wie in vielen anderen Wissenschaften auch, gibt es in der Mathematik eine eigene Fachsprache. Teile davon, hast du
bereits in der Unterstufe kennen gelernt.
Aussagen sind Behauptungen, die entweder wahr oder falsch sein können.
Sie beinhalten Eigenschaften und Beziehungen zwischen z.B. Zahlen oder geometrischen Figuren. Sie können sich auf
eine Eigenschaft von einem einzelnen "Objekt" beziehen oder auf eine Eigenschaft von mehreren Objekten.
Bezieht sich eine Aussage auf die Eigenschaft mehrerer Objekte, so nennt man die Gesamtheit dieser Objekte die
Grundmenge G (meist $NN, ZZ, QQ, RR$) der Aussage. Formuliert werden diese Aussagen mit Hilfe
von Variablen und Quantoren:
| $AA$ | Für alle ... | Allquantor | Allaussagen |
| $EE$ | Für mindestens ein ... | Existenzquantor | Existenzaussagen |
| $EE!$ | Für genau ein ... | Eindeutigkeitsquantor |
Beispiel Allaussagen: Alle geraden natürlichen Zahlen sind durch 2 teilbar; formal: $AA x in NN_(g) : 2 | x$
Beispiel Existenzaussage: Es gibt mindestens eine ganze Zahl zwischen 4 und 10, die
Primzahl ist; formal: $EE x in ZZ, 4 < x < 10 : x in$
![]()
Eine Allaussage ist falsch, sobald man ein einziges Gegenbeispiel gefunden hat (man falsifiziert!
Eine Existenzaussage ist wahr, sobald man ein einziges Beispiel angeben kann (man verifiziert)!
Das Gegenteil einer Aussage ist ihre Negation bzw. Gegenaussage:
Aussage a - Negation $not$ a (non a oder nicht a). Statt des Negationssymbols kann
man auch ein Symbol durchstreichen, um eine Aussage zu verneinen, z.B. $!in$ oder das Symbol der gegenteiligen
Eigenschaft verwenden, z.B. < statt $>=$.
Negiert man eine Allaussage, so führt dies zu einer Existenzaussage bezüglich der gegenteiligen Eigenschaft.
Negiert man eine Existenzaussage, so führt dies zu einer Allaussage bezüglich der gegenteiligen Eigenschaft.
Beispiele:
- Alle ganzen Zahlen sind durch 5 teilbar. formal: $AA x in ZZ : 5 | x$ (falsche Aussage,
5
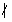 2);
Negation: $not(AA x in ZZ : 5 | x)$ oder $EE x in ZZ : not (5 | x)$
2);
Negation: $not(AA x in ZZ : 5 | x)$ oder $EE x in ZZ : not (5 | x)$ - Es gibt mindestens eine rationale Zahl zwischen 6 und 7. formal: $EE x in QQ : 6 < x < 7$ (wahre Aussage)
- Es gibt genau eine ganze Zahl, deren Quadrat gleich der Zahl ist. formal $EE! x in ZZ : x^2 = x$ (falsche Aussage, weil $0^2 = 0$ und $1^2=1$); Negation: $AA x in ZZ : x^2$ ≠ x oder $not(EE! x in ZZ : x^2 = x)$
Mengen - Wiederholung und Vertiefung
Zahlenmengen im Überblick:
$NN$ ... Menge der natürlichen Zahlen ${0, 1, 2, 3, ...}$
$ZZ$ ... Menge der ganzen Zahlen ${..., -3, -2, -1, 0, 1, 2, 3, ...}$
$QQ$ ... Menge der rationalen Zahlen (ganze Zahlen und Brüche)
$RR$ ... Menge der reellen Zahlen (alle Zahlen)
Aufzählendes und beschreibendes Verfahren siehe erste Klasse
Was Mengen mit Aussagen zu tun haben:
Erfüllen Elemente der Grundmenge eine gegebene Eigenschaft, so bilden diese eine Teilmenge A der
Grundmenge G. Jene Elemente, die die Eigenschaft nicht erfüllen, bilden ebenfalls eine Teilmenge, die so genannte
Komplementärmenge A' (Ergänzungsmenge). Die Mengen A und A' ergänzen einander zur Grundmenge G.
Es gilt: A = G \ A' (A ist G ohne A') und A' = G \ A
Beispiel: Grundmenge $NN$, Eigenschaft $x >= 4$; $text(A)={4, 5, 6, ...}; text(A') = {0, 1, 2, 3}$
Die Menge der reellen Zahlen und ihre Teilmengen, kann man im aufzählenden Verfahren nicht angeben, aber mit Hilfe von Intervallen. Diese werden mit eckigen Klammern [ und ] angegeben. Zusätzlich können Teilmengen der reellen Zahlen auch auf der Zahlengeraden dargestellt werden. Dabei werden Randpunkte, die zur Menge gehören mit vollen Punkten gekennzeichnet und Randpunkte, die nicht zur Menge gehören, mit leeren Punkten.
| Beschreibung | Intervall | Name | Zahlengerade | Bild |
|---|---|---|---|---|
| 2 $<=$ $x$ $<=$ 9 | $[$2; 9$]$ | abgeschlossenes Intervall | beide Punkte voll | |
| 2 < $x$ < 9 | $]$2; 9$[$ | offenes Intervall | beide Punkte leer | |
| 2 $<=$ $x$ < 9 | $[$2; 9$[$ | links abgeschlossenes, rechts offenes Intervall | linker Punkt voll, rechter Punkt leer | |
| 2 < $x$ $<=$ 9 | $]$2; 9$]$ | links offenes, rechts abgeschlossenes Intervall | linker Punkt leer, rechter Punkt voll | |
| $-oo$ < $x$ $<=$ 9 | $]$$-oo$; 9$]$ | rechts abgeschlossenes, unbeschränktes Intervall | Pfeil nach links, rchter Punkt voll | |
| $-oo$ < $x$ < 9 | $]$$-oo$; 9$[$ | rechts offenes, unbeschränktes Intervall | Pfeil nach links, rechter Punkt leer | |
| 2 $<=$ $x$ < $oo$ | $[$2; $oo$$[$ | links abgeschlossenes, unbeschränktes Intervall | linker Punkt voll, Pfeil nach rechts | |
| 2 < $x$ < $oo$ | $]$2; $oo$$[$ | links offenes, unbeschränktes Intervall | linker Punkt leer, Pfeil nach rechts |
Im Falle, dass die Grundmenge $ZZ$ oder $NN$ ist, werden die einzelnen Zahlen nur als Punkte auf der Zahlengeraden dargestellt!
Beziehungen zw. Mengen und Aussagen
Haben 2 Mengen genau dieselben Elemente, so heißen sie gleich, formal: A = B.
