Sabine Tullits - Rund um die Schule

Für die richtige Darstellung der Inhalte muss JavaScript aktiviert sein!

Das Zehnersystem

Zu Anfang ein paar Fragen:
Du leerst dein Sparschwein und willst alle Münzen zählen. Wie wirst du vorgehen, wenn du möglichst schnell fertig werden möchtest?

Wie viele Ziffern gibt es?

Wie viele Zahlen gibt es?

Das Zahlensystem, in dem du rechnest, heißt dekadisches System, weil immer 10 Einheiten zur nächstgrößeren Einheit zusammengefasst werden können (siehe Frage 1). Das heißt 10 1-Cent-Münzen ergeben 10 Cent. 10 10-Cent-Münzen ergeben 1 Euro usw. So wie es beim Geld funktioniert, funktioniert es auch bei den Zahlen. 10 Einer ergeben 1 Zehner, 10 Zehner ergeben 1 Hunderter usw.

Die Antwort auf Frage 2 und 3 haben dich vielleicht anfangs verwirrt, aber jede Zahl, besteht eigentlich aus Ziffern. Und jede dieser Ziffern hat einen ganz bestimmten Stellenwert, je nachdem, wo sie in der Zahl steht.

Beispiel: 456 - die Ziffer 6 hat den Stellenwert Einer, die Ziffer 5 hat den Stellenwert Zehner und die Ziffer 4 hat den Stellenwert Hunderter.

Beim Anschreiben von großen Zahlen ist es hilfreich, wenn man sie in Dreiergruppen anschreibt - immer von hinten nach vorne, also von den Einern weg!

Beispiel: 4520384892 ist schwer zu lesen. Einfacher ist es so: 4 520 384 892
4 Milliarden 520 Millionen 384 Tausend 892

Damit man nicht so viel schreiben muss, gibt es für jeden Stellenwert eine Abkürzung; achte auf die Groß- und Kleinschreibung!

B	Billion
HMd	Hundertmilliarden
ZMd	Zehnmilliarden
Md	Milliarden
HM	Hundertmillionen
ZM	Zehnmillionen
M	Millionen
HT	Hunderttausend
ZT	Zehntausend
T	Tausender
H	Hunderter
Z	Zehner
E	Einer

Um Zahlen mit Hilfe von dekadischen Einheiten (Einer, Zehner, usw.) anzuschreiben, oder ohne dekadische Einheiten zu schreiben, kannst du eine Stellenwerttafel benutzen. Diese kannst du dir leicht selber zeichnen, sie sollte so aussehen:

		Milliarden			Millionen			Tausender
	B	HMd	ZMd	Md	HM	ZM	M	HT	ZT	T	H	Z	E
Beispiel 1				9	5	8	7	6	0	2	5	8	1
Beispiel 2		7	0	9	0	1	0	3	0	7	0	0	5

Zur Verwendung der Stellenwerttafel:
Beispiel 1: Schreibe die Zahl mit ihrem Stellenwert an: 9 587 602 581
Lösung: 9 Md 5 HM 8 ZM 7 M 6 HT 2 T 5 H 8 Z 1 E
BEACHTE: 0 ZT wird bei der Lösung NICHT angeschrieben!
TIP: Beginne beim Eintragen immer hinten!

Beispiel 2: Schreibe als Zahl: 7 HMd 9 Md 1 ZM 3 HT 7 T 5 E
Lösung: 709 010 307 005
BEACHTE: Leerstehende Felder werden mit 0 aufgefüllt!

Runden

Runden bedeutet, einen genauen Wert näherungsweise, also ungefähr, anzugeben. Dies kann man z.B. bei Höhenangaben verwenden: Der Großglockner ist rund (ungefähr) 4 000 m hoch (genauer Wert: 3 798 m). Um zu kennzeichnen, dass man gerundet hat, verwendet man ein eigenes Symbol, das Rundungssymbol $~~$.

Man kann eine Zahl auf jede in ihr vorkommende Stelle runden (außer auf die Einer). Es gilt dabei folgende Rundungsregel:

Bei den Ziffern 0, 1, 2, 3, 4 wird abgerundet und bei den Ziffern 5, 6, 7, 8, 9 wird aufgerundet. Abrunden bedeutet, die Stelle, auf die man runden muss, bleibt gleich, aufrunden heißt, die Stelle, auf die man runden muss, wird um 1 erhöht.

Ob man aufrunden oder abrunden muss, entscheidet die nächstfolgende (niedrigere) Stelle. Das heißt, möchte man auf die Zehner runden, entscheidet die Einerstelle; möchte man auf die Hunderter runden, entscheidet die Zehnerstelle usw. Alle Stellen hinter der, auf die man gerundet hat, werden zu 0.

Beim Runden begeht man immer einen Rundungsfehler (RF). Diesen kann man berechnen, indem man die kleinere von der größeren Zahl abzieht.

Beispiel abrunden: 5 836 $~~$ 5 800 (gerundet auf H), RF: 5 836 - 5 800 = 36

Beispiel aufrunden: 5 861 $~~$ 5 900 (gerundet auf H), RF: 5 900 - 5 861 = 39

Ordnen und Vergleichen

Alle Zahlen, die du bis jetzt kennst, haben einen bestimmten Namen: natürliche Zahlen: 0, 1, 2, 3, ... Aber wie viele natürliche Zahlen gibt es?

Vorgänger: Zahl, die direkt vor der natürlichen Zahl steht
Nachfolger: Zahl, die direkt hinter der natürlichen Zahl steht

54	55	56
Vorgänger	Natürliche Zahl	Nachfolger

Überlege: Hat jede natürliche Zahl einen Vorgänger?

In der Mathematik dienen oft Symbole als Abkürzung, ein Symbol hast du bereits kennen gelernt, das Rundungssymbol. Beim Ordnen und Vergleichen benötigt man 2 weitere Symbole:

$<$: Kleiner-Symbol, ... ist kleiner als ...
$<=$: Kleiner-Gleich-Symbol, ... ist kleiner oder gleich als ...
$>$: Größer-Symbol, ... ist größer als ...
$>=$: Größer-Gleich-Symbol, ... ist größer oder gleich als ...

Beispiel: 4 ist kleiner als 8 wird zu 4 < 8 oder 13 ist größer als 9 wird zu 13 > 9

Eine derartige Darstellung mit diesen Symbolen nennt man Ungleichung. Werden mehrere Zahlen mit dem Kleiner- oder Größer-Symbol verbunden, spricht man von einer Ungleichungskette: 5 < 9 < 15 < 23 < 48

Zahlenstrahl

Auf einem Zahlenstrahl können natürliche Zahlen eingezeichnet werden. Dabei erhält jede natürliche Zahl genau einen Punkt. Der Zahlenstrahl beginnt normalerweise immer bei 0. Die Strecke, die du zwischen 0 und 1 wählst, heißt Einheitsstrecke. Diese kann 1 cm sein, aber auch 2 cm oder 5 mm. Um anzudeuten, dass der Zahlenstrahl immer weiter geht, macht man am Ende immer einen Pfeil!

Beispiele:
Einheitsstrecke: 1cm Zahlenstrahl mit Einheitsstrecke 1cm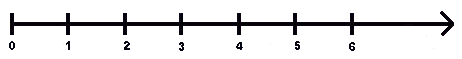
Einheitsstrecke: 2cm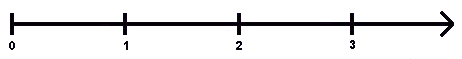
Einheitsstrecke: 5mm

Ein Zahlenstrahl muss aber nicht bei 0 beginnen! Möchte man zum Beispiel nur Zahlen zwischen 250 und 300 einzeichen, so lässt man den Zahlenstrahl etwas vor der ersten Zahl beginnen:

Beispiel: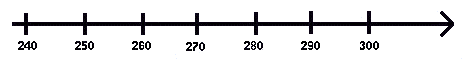 Zahlenstrahl, der nicht bei 0 beginnt

Beachte: Wenn du einen Zahlenstrahl in dein Heft zeichnest, dann sollte er mindestens 7 cm lang sein! Es ist übrigens nicht erlaubt, einen Zahlenstrahl über 2 Zeilen zu zeichnen! Sollte es sich nicht anders ausgehen, musst du eine kleinere Einheitsstrecke wählen!

Römische Zahlen

Die Römer verwendeten andere Zahlzeichen als wir es heute tun. Diese Zeichen sehen wie folgt aus:

I	V	X	L	C	D	M
1	5	10	50	100	500	1 000

Um eine Zahl nun mit römischen Zahlzeichen darzustellen, musst du ein guter Kopfrechner sein! Die Zahlen ergeben sich durch Nebeneinanderschreiben der benötigten Zeichen.

Beispiel 1: 38 = 10 + 10 + 10 + 5 + 1 + 1 + 1 = XXXVIII

Beispiel 2: 266 = 100 + 100 + 50 + 10 + 5 + 1 = CCLXVI

Natürliche muss man auch hier einige Regeln beachten:

Regel 1: Es dürfen nie mehr als 3 gleiche Zeichen nebeneinander stehen!

Regel 2: Steht ein Zeichen mit kleinerem (oder gleichem) Wert hinter einem Zeichen mit größerem Wert, so werden beide addiert!

Beispiel:

1000

500

100

1 715

Regel 3: Steht ein Zeichen mit größerem Wert hinter einem Zeichen mit kleinerem Wert, so werden beide subtrahiert!

Beispiel:

M	C	D	L	I	X
1000	100	500	50	1	10
+	-		+	-		1 459

Regel 4: Es ist nicht erlaubt sehr große und sehr kleine Zahlzeichen nebeneinander zu schreiben!

Beispiel (falsch): 98 = IIC
Beispiel (richtig): 98 = XCVIII

Beispiel (falsch): 999 = IM
Beispiel (richtig): 999 = CMXCIX

Möchte man unsere Zahlen in römische Zahlen verwandeln, muss man diese 4 Regeln ebenfalls beachten!

Gleichungen und Ungleichungen

Rechnungen wie diese 17 + = 45 kennst du sicherlich schon aus der Volksschule. Das steht hier für eine Zahl, die du finden musst, und heißt Platzhalter. Normalerweise schreibt man anstatt des einen Buchstaben, dieser heißt Variable. Die Variable erfüllt dabei den gleichen Zweck wie das Kästchen. Die obige Rechnung würde damit so aussehen:
17 + x = 45

Eine derartige Rechnung wird Gleichung genannt, weil links und rechts vom Istgleich-Zeichen etwas steht - die beiden Seiten sollen gleich sein.

Kannst du berechnen, welche Zahl du für das x einsetzen musst?

Beim Lösen einer Gleichung, ist es sinnvoll, wenn man einen Zwischenschritt angibt. Hier schreibt man an, wie man die Variable berechnet. Dies soll nun an einigen Beispielen verdeutlicht werden:

$34 + a = 50$ $a = 50 - 34$ $a = 16$	$ b + 123 = 200$ $b = 200 - 123$ $b = 77$	$67 - x = 23$ $x = 67 - 23$ $x = 44$	$y - 41 = 10$ $y = 10 + 41$ $y = 51$

$m * 7 = 35$ $m = 35 : 7$ $m = 5$	$12 * u = 120$ $u = 120 : 12$ $u = 10$	$69 : s = 23$ $s = 69 : 23$ $s = 3$	$z : 4 = 51$ $z = 51 * 4$ $z = 204$

Nun kann es sein, dass in einer Gleichung eine Punktrechnung und eine Strichrechnung vorkommen. Hier kannst du dir mit einer kleinen Geschichte helfen:

$2 * x + 15 = 31$	Stell dir vor, 2 und x sind verheiratet und wohnen gemeinsam mit 15 in einem Haus. Da das Paar frisch verliebt ist, soll 15 ausziehen, auf die andere Straßenseite zu 31.
$2 * x = 31 - 15$
$2 * x = 16$	Kaum ist 15 nun aus dem Haus, beginnt das Paar zu streiten und sie trennen sich.
$x = 16 : 2$
$x = 8$	Gleichung gelöst!

DAS HEIßT: Trenne nie zuerst die Punktrechnung, egal ob es sich um eine Mulitiplikation oder Division handelt!

Ungleichungen hast du schon beim Ordnen und Vergleichen kennen gelernt. Gleichungen haben genau eine Lösung, Ungleichungen werden aber meistens von mehreren Zahlen erfüllt! Diese Zahlen schreibt man in eine sogenannte Lösungsmenge.

Beispiel: x ist kleiner als 5 - als Ungleichung geschrieben: $x < 5$
Lösungsmenge $L = {0, 1, 2, 3, 4}$

Wie du siehst verwendet man für die Lösungsmenge besondere Klammern, sie heißen Mengenklammern oder geschwungene Klammern.

Um auf die richtige Lösungsmenge zu kommen, musst du dir einfach nur eine Frage stellen:
Welche Zahlen sind kleiner (größer) als die angegebene Zahl?

Beispiel: $x > 12$ Welche Zahlen sind größer oder gleich als 12?
$L = {12, 13, 14, 15, 16, ...}$

In diesem Beispiel wäre es nicht möglich, alle Zahlen, die diese Ungleichung erfüllen, aufzuschreiben. Daher gibt man die ersten 5 Zahlen an und macht dann 3 Punkte.

Vielleicht hast du auch den Unterschied zwischen dem > (<)und dem ≥ (≤)erkannt: Beim > (<) wird die Zahl selbst nicht genommen, beim ≥ (≤) schon!

Mengen

In der Mathematik gibt es viele Mengen, aber was ist das überhaupt?

Stell' dir vor, du hast einen Sack voll Äpfel. Alle diese Äpfel bilden eine Menge: die Menge der Äpfel im Sack.
Oder: Alle Schüler der 4A Klasse bilden eine Menge.

In einer Menge sind zusammengehörige Objekte, die alle die gleichen Eigenschaften haben.
Zahlen, die zu einer Menge gehören, nennt man Element.
Symbole: $in$ - ist Element von
$!in$ - ist kein Element von

Im ersten Beispiel wäre die gemeinsame Eigenschaft Äpfel, im 2. Beispiel wäre das, dass alle diese Kinder in die 4A Klasse gehen.

Du weißt bereits, dass es unendlich viele natürliche Zahlen gibt, diese werden zu einer Menge zusammengefasst:

$NN$ ... Menge der natürlichen Zahlen {0, 1, 2, 3, 4, 5}
$NN_u$ ... Menge der ungeraden natürlichen Zahlen {1, 3, 5, 7, 9, ...}
$NN_g$ ... Menge der geraden natürlichen Zahlen {2, 4, 6, 8, 10, ...}

Nun gibt es in der Mathematik auch verschiedene Möglichkeiten, Mengen anzugeben, man spricht von Mengenschreibweisen. Wie diese funktionieren, sei an einem Beispiel gezeigt:

Beispiel: Gib alle Zahlen an, die zwischen 49 und 54 liegen.
$A = {50, 51, 52, 53}$
Dabei ist A der Name der Menge (irgendein Großbuchstabe) und in die Mengenklammer kommen dann alle Zahlen, die gefordert sind. Dieses Verfahren heißt aufzählendes Verfahren, weil die Zahlen einzeln aufgezählt werden.

Man kann aber auch anders vorgehen, und die gewünschten Zahlen beschreiben, was uns zum beschreibenden Verfahren bringt:

Beispiel: $A = {x in NN | 49 < x < 54 }$ - Was heißt das nun?
   x ... steht für die Zahlen, die man einsetzen könnte
  $in$ ... ist ein Element von
   $NN$ ... Menge der natürlichen Zahlen
   | ... für die gilt
   49 < x < 54 ... Bedingung, die erfüllt werden soll
Gesamt ergibt sich: x ist ein Element der natürlichen Zahlen, für die gilt, dass 49 kleiner als x ist und x kleiner als 54, also genau die gewünschten Zahlen.

Achtung: Achte darauf, welche Symbole du jeweils verwendest! < und > bedeuten, dass die Zahlen nicht zur Menge gehören!

Du weißt nun schon ein wenig über Mengen, aber es gibt noch spezielle Arten von Mengen, wie z.B. die Durchschnittsmenge, die Vereinigungsmenge und die Teilmenge.
Stell' dir vor, Max und Moritz gehen in einen Fußballverein und in einen Schwimmverein, Fritz und Franz nur in den Fußballverein, Susi und Sandra nur in den Schwimmverein. Dies kann man grafisch so darstellen (in einem so genannten Mengenbild):

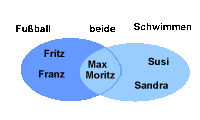
Durchschnitt

Da Max und Moritz in beide Vereine gehen, stehen sie in der Mitte der beiden Kreise. Die Kreise stehen für die jeweiligen Vereine bzw. Mengen. Max und Moritz bilden hier die Durchschnittsmenge.

Die Durchschnittsmenge zweier Mengen A und B besteht aus den Elementen, die sowohl zu der einen als auch zu der anderen Menge gehören. Symbolisch: A $nnn$ B

Alle Kinder, also Max, Moritz, Fritz, Franz, Susi und Sandra zusammen bilden die Vereinigungsmenge. Hier ist es egal, in welchen Verein sie gehen.

Die Vereinigungsmenge zweier Mengen A und B besteht aus jenen Elementen, die entweder zu A oder zu B oder zu beiden Mengen gehören. Symbolisch: A $uuu$ B

Beispiel Durchschnittsmenge: Gegeben sind 2 Mengen A und B:
   A = {3, 7, 9, 12, 22}
   B = {5, 9, 11, 12, 22, 25}
   A $nnn$ B = {9, 12, 22}, weil diese Zahlen in beiden Mengen vorkommen!

Beispiel Vereinigungsmenge: Gegeben sind dieselben Mengen wie oben:
A $uuu$ B = {3, 5, 7, 9, 11, 12, 22, 25}, alle vorkommenden Zahlen bilden diese Menge!

Nun fehlt nur noch die Teilmenge:

Man spricht von einer Teilmenge, wenn alle Elemente dieser Menge auch Elemente der (übergeordneten) Menge sind. Symbolisch: T $sub$ M

Beispiel Teilmenge: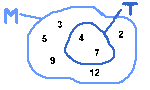 ${4, 7} sub {2, 3, 4, 5, 7, 9, 12}$

Das Wichtigste zu diesem Kapitel

Zehnersystem

Das Zahlensystem, in dem du rechnest, heißt dekadisches System, weil immer 10 Einheiten zur nächstgrößeren Einheit zusammengefasst werden können.

Stellenwerttafel:

Milliarden

Millionen

Tausender

HMd

ZMd

Runden

Beim Runden begeht man immer einen Rundungsfehler (RF). Diesen kann man berechnen, indem man die kleinere von der größeren Zahl abzieht.

Ordnen und Vergleichen

<: Kleiner-Symbol, ... ist kleiner als ...
≤: Kleiner-Gleich-Symbol, ... ist kleiner oder gleich als ...
>: Größer-Symbol, ... ist größer als ...
≥: Größer-Gleich-Symbol, ... ist größer oder gleich als ...

Zahlenstrahl

Römische Zahlen

I	V	X	L	C	D	M
1	5	10	50	100	500	1 000

Regel 1: Es dürfen nie mehr als 3 gleiche Zeichen nebeneinander stehen!

Regel 2: Steht ein Zeichen mit kleinerem (oder gleichem) Wert hinter einem Zeichen mit größerem Wert, so werden beide addiert!

Regel 3: Steht ein Zeichen mit größerem Wert hinter einem Zeichen mit kleinerem Wert, so werden beide subtrahiert!

Regel 4: Es ist nicht erlaubt sehr große und sehr kleine Zahlzeichen nebeneinander zu schreiben!

Gleichungen und Ungleichungen

Eine Rechnung wie 2 + x = 54 wird Gleichung genannt, weil links und rechts vom Istgleich-Zeichen etwas steht - die beiden Seiten sollen gleich sein. Der Buchstabe - hier x - heißt Variable (Platzhalter)

Trenne nie zuerst die Punktrechnung, egal ob es sich um eine Mulitiplikation oder Division handelt!

Gleichungen haben genau eine Lösung, Ungleichungen werden aber meistens von mehreren Zahlen erfüllt! Diese Zahlen schreibt man in eine sogenannte Lösungsmenge.

Mengen

Die Durchschnittsmenge zweier Mengen A und B besteht aus den Elementen, die sowohl zu der einen als auch zu der anderen Menge gehören. Symbolisch: A $nnn$ B

Die Vereinigungsmenge zweier Mengen A und B besteht aus jenen Elementen, die entweder zu A oder zu B oder zu beiden Mengen gehören. Symbolisch: A $uuu$ B

Man spricht von einer Teilmenge, wenn alle Elemente dieser Menge auch Elemente der (übergeordneten) Menge sind. Symbolisch: T $sub$ M