Gehe zu:

Multiplizieren mit einstelligen Zahlen

Was bedeutet eigentlich multiplizieren? Diese Rechenart ist nichts anderes, als eine Vereinfachung der Addition!

Beispiel: 23 + 23 + 23 + 23 =
      Diese Addition kann man viel einfacher berechnen, nämlich mit 23 · 4 = 92

Daher folgt:

Die Multiplikation entspricht der Addition gleicher Summanden.

Auch hier gibt es ganz bestimmte Namen für die einzelnen Zahlen:

Bezeichnungen bei der Multiplikation:
7 · 4 = 28
  (1.) Faktor, Multiplikand   (2.) Faktor, Multiplikator   Produkt  
Die Zahlen bei der Multiplikation heißen Faktoren, das Ergebnis Produkt.         

Du kennst sicherlich die Mal-Reihe von 4: 4, 8, 12, 16, 20, usw. Diese Zahlen nennt man Vielfache von 4.

Die Vielfachen einer Zahl erhält man, indem man sie mit 1, 2, 3, usw. multipliziert.

Beispiel: Nenne die ersten 5 Vielfachen von 6: 6, 12, 18, 24, 30.

Das Multiplizieren mit einstelligen Zahlen ist relativ einfach. Bisher bist du wahrscheinlich gewöhnt, auch hier einen Strich zu machen und das Ergebnis darunter zu schreiben. Das benötigt zum einen viel Platz im Heft und ist zum anderen nicht nötig! Wenn du mit einstelligen Zahlen multiplizierst, ist es oft besser in der Zeile zu rechnen! Wie beim Addieren und Subtrahieren in der Zeile kannst du die Zifferen, mit denen du schon gerechnet hast, unterstreichen (oder abhaken). Wichtig ist nur, dass du beim Aufschreiben des Ergebnisses von hinten anfängst zu schreiben.

Beispiel: Statt so: untereinander schreiben machste du es einfach so: multiplizieren in der Zeile

Und nun etwas sehr einfaches: Du weißt hoffentlich noch, was dekadische Einheiten sind, oder? Wenn nicht, dann lies im Kapitel Natürliche Zahlen nach! Überlege, was passiert, wenn du eine Zahl mit dekadischen Einheiten multiplizierst!

Beispiel:
     45 · 10 = 450
     45 · 100 = 4 500
     45 · 1000 = 45 000

Fällt dir etwas auf? Wenn ja, dann ist die nächste Regel sehr einfach zu merken:

Natürliche Zahlen werden mit dekadischen Einheiten multipliziert, indem man so viele Nullen anhängt, wie in der dekadischen Einheit vorkommen.

Sollte es sich um ein Vielfaches einer dekadischen Einheit handeln, z.B. 400, so wird die Zahl mit 4 multipliziert und dann werden die Nullen angehängt.

Beispiel: 593 · 400 = 237 200

Multiplizieren mit mehrstelligen Zahlen

Zu einer Multiplikation gehört mehr als nur das Ausrechnen, man sollte auch abschätzen können, wie groß das Ergebnis in etwa ist. Damit erhält man auch nach dem Berechnen eine Rückmeldung, ob das erhaltene Ergebnis überhaupt stimmen kann. Dafür gibt es 2 Möglichkeiten:

Möglichkeit 1- der Überschlag: Dazu werden die beiden vorkommenden Faktoren auf die höchste Stelle gerundet. Dann reicht es, die beiden ersten Ziffern beider Zahlen zu multiplizieren und so viele Nullen anzuhängen, wie in beiden Faktoren vorkommen.
Beispiel: 5 972 · 73    Überschlag (Ü): 6 000 · 70 = 420 000
Das heißt: Das Ergebnis der Rechnung muss ungefähr 420 000 betragen.
Das Ergebnis der Multiplikation ist 435 956 - hier liegt natürlich ein Fehler vor, da wir gerundet haben! Der Fehler ist um so größer, je mehr gerundet wurde!

Möglichkeit 2 - die Schranken: Von beiden Faktoren wird die nächstkleinere und nächstgrößere "Zehnerzahl" (von der höchsten vorkommenden Stelle) angegeben. Dann werden die beiden kleineren und die beiden größeren miteinander multipliziert. Das Ergebnis der Rechnung muss dann zwischen diesen beiden erhaltenen Zahlen liegen.
Beispiel: 5 972 · 73
     5 000 < 5 972 < 6 000  und   70 < 73 < 80
     5 000 · 70 = 350 000
     6 000 · 80 = 480 000
Das heißt: Das Ergebnis der Rechnung muss zwischen 350 000 und 480 000 liegen.

Wozu dienen nun Überschlag und Schranken?
Bei Multiplikationen mit größeren Zahlen verrechnet man sich sehr schnell, das ist dir sicherlich auch schon passiert! Siehst du nun, dass dein Ergebnis nicht mit dem Überschlag übereinstimmt oder nicht zwischen den ausgerechneten Schranken liegt, dann liegt irgendwo ein Fehler. Überprüfe zuerst immer den Überschlag bzw. die Schranken - das geht schneller! Stimmen diese, dann rechne die Multiplikation noch einmal nach!

Das eigentliche Multiplizieren: Das kleine 1x1 solltest du auf jeden Fall gut beherrschen. Begonnen wird mit der 1. Ziffer des zweiten Faktors, dann mit der nächsten Ziffer des zweiten Faktors, wobei du beim Anschreiben eine Stelle nach rechts rückst. Dann die nächste Ziffer des zweiten Faktors usw. Achte darauf, dass der zweite Faktor die kleinere der beiden Zahlen ist, dann wird die Rechnung kürzer! Zum Schluss wird addiert und du bist fertig.

Ein häufiger Fehler ist das falsche Untereinanderschreiben der einzelnen Zeilen. Um das zu vermeiden, kannst du in der vorhergehenden Zeile eine 0 oder einen Punkt machen.

Beispiel: Falsch: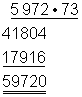        Richtig: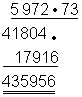
Wenn du einen Überschlag oder Schranken gemacht hast, dann erkennst du leicht, dass die erste Rechnung nicht stimmen kann und daher ist es so wichtig, Überschlag oder Schranken vor dem Berechnen zu machen!!

In Textaufgaben erkennt man, dass man multiplizieren muss, wenn eines oder mehrere der folgenden Wörter vorkommen: Multiplikation, multiplizieren, Produkt, Faktor, vervielfachen, Vielfaches, das Doppelte, Dreifache, Vierfache, ...

Dividieren durch einstellige Zahlen

Wie bei allen Grundrechnungsarten haben auch die Zahlen bei der Division bestimmte Namen:

Bezeichnungen bei der Division:
45 : 5 = 9
  Dividend   Divisor   Quotient  
Die erste Zahl bei der Division heißt Dividend, die zweite Divisor und das Ergebnis Quotient.

Bei einer Division kann man zwischen 2 Arten unterscheiden: Messen und Teilen

Messen: eine Größe (z.B. Euro, cm, kg) wird durch dieselbe Größe dividiert, man erhält als Ergebnis eine Zahl
Beispiel: Ein Bauer hat 140 kg Äpfel geerntet und möchte diese in Säcken zu 7 kg verkaufen. Wie viele Säcke kann der Bauer mit seiner Ernte verkaufen?
140 kg : 7 kg = 20 (Säcke) => Der Bauer kann 20 Säcke verkaufen.

Teilen: eine Größe wird durch eine Zahl dividiert, man erhält als Ergebnis eine Größe
Beispiel: Ein Bauer hat 140 kg Äpfel geerntet und möchte 20 Säcke verkaufen. Wie viel kg Äpfel muss er in einen Sack packen?
140 kg : 20 = 7 kg => Er muss 7 kg Äpfel in einen Sack geben.

Du kannst eine Addition, eine Subtraktion und eine Multiplikation mit einer einstelligen Zahl nun schon in der Zeile durchführen. Genauso funktioniert auch eine Division mit einer einstelligen Zahl. Denke dir den Rest und hake die Zahlen, die du schon verwendet hast, einfach ab (oder mache einen Punkt darunter).
Beispiel (vorher): 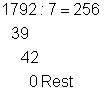     Beispiel (jetzt):

Nun stellst du dir vielleicht die Frage: Kann ich das Ergebnis einer Division irgendwie überprüfen? NATÜRLICH! Wie bei der Addition und Subtraktion gibt es auch hier eine Probe - eine Multiplikation. Du musst das Ergebnis der Division (den Quotienten) mit dem Divisor multiplizieren.

Zusammenhang zwischen Multiplikation und Division
Die Multiplikation ist die Umkehrung der Division. Dies kann für die Probe verwendet werden. Für die Probe wird der Quotient mit dem Divisor multipliziert, das Ergebnis ist der Dividend.

Ist es erlaubt, durch jede natürliche Zahl zu dividieren? NEIN! Die Division durch 0 ist sinnlos! Warum ist das so? Angenommen, wir hätten folgende Division: 5 : 0 = ?. Mögliche Ergebnisse wären 5 oder 0. Wenn man nun die Probe durchführt, erhält man folgendes: 5 · 0 = 0 und im zweiten Fall 0 · 0 = 0. Aber man erhält nie die Zahl 5 als Ergebnis. Daher ist die Division durch 0 sinnlos!

Die Division durch Null ist sinnlos!
Dividiert man eine Zahl durch 0, so ist das Ergebnis immer 0! (0 : 5 = 0)

Dividieren durch mehrstellige Zahlen

Divisionen mit Rest

Rechenregeln

Das Wichtigste zu diesem Kapitel