Gehe zu:

Für die richtige Darstellung der Inhalte muss JavaScript aktiviert sein!

Einheiten und deren Umrechnung

Längenmaße: Grundeinheit ist das Meter
Abkürzungen: km = Kilometer, m = Meter, dm = Dezimeter, cm = Zentimeter, mm = Millimeter
Umrechnung: 1 km = 1 000 m, 1 m = 10 dm, 1 dm = 10 cm, 1 cm = 10 mm

km     m dm cm mm

Massenmaße: Grundeinheit ist das Kilogramm
Abkürzungen: t = Tonne, kg = Kilogramm, dag = Dekagramm, g = Gramm, dg = Dezigramm cg = Zentigramm, mg = Milligramm
Umrechnung: 1 t = 1 000 kg, 1 kg = 100 dag, 1 dag = 10 g, 1 g = 10 dg, 1 dg = 10 cg, 1 cg = 10 mg

t     kg   dag g dg cg mg

Zeitmaße: Grundeinheit ist die Sekunde
Abkürzungen: d = Tag, h = Stunde, min = Minute, s = Sekunde
Umrechnung: 1 Jahr = 12 Monate (365 Tage), 1 Monat = (28) 30 (31) Tage, 1 Woche = 7 d, 1 d = 24 h, 1 h = 60 min, 1 min = 60 s, 1 h = 3 600 s

Flächenmaße: Grundeinheit ist das Quadratmeter
Abkürzungen: $km^2$ = Quadratkilometer, ha = Hektar, a = Ar, $m^2$ = Quadratmeter, $dm^2$ = Quadratdezimeter, $cm^2$ = Quadratzentimeter, $mm^2$ = Quadratmillimeter
Umrechnung:1 $km^2$ = 100 ha, 1 ha = 100 a, 1 a = 100 $m^2$, 1 $m^2$ = 100 $dm^2$ 1 $dm^2$ = 100 $cm^2$, 1 $cm^2$ = 100 $mm^2$

$km^2$   ha   a   $m^2$   $dm^2$   $cm^2$   $mm^2$

Raummaße: Grundeinheit ist das Kubikmeter
Abkürzungen: $m^3$ = Kubikmeter, $dm^3$ = Kubikdezimeter, $cm^3$ = Kubikzentimeter, $mm^3$ = Kubikmillimeter, hl = Hektoliter, l = Liter, dl = Deziliter, cl = Zentiliter, ml = Milliliter
Umrechnung: 1 $m^3$ = 1000 $dm^3$, 1 $dm^3$ = 1000 $cm^3$, 1 $cm^3$ = 1000 $mm^3$, 1 hl = 100 l, 1 l = 10 dl, 1 dl = 10 cl, 1 cl = 10 ml, 1 $dm^3$ = 1 l, 1 $cm^3$ = 1 ml

$m^3$     $dm^3$     $cm^3$     $mm^3$
  hl   l dl cl ml      

Andere Einheiten

Klafter: 1 Klafter = 1,829 m

Elle: 1 Elle = 1,143 m

Spanne: 1 Spanne = 22,9 cm

Yard: 1 yd = 914,4 mm (englisches Längemaß)

Foot: 1 ft = 304,8 mm (englisches Längemaß)

Inch: 1 inch = 25,4 mm (englisches Längenmaß)

Seemeile: 1 sm = 1,852 km

Wiener Fuß: 1 Wiener Fuß = 0,316 m

Karat: 1 Karat = 0,2 g

Quadratmeile: 1 Quadratmeile = 2,589913 km²

österreichisches Joch: 1 Joch ≈ 0,58 ha

Barrel: 1 bbl = 158,8 l

Gallon: 1 gal = 3,78 l

Rechengesetze / Rechenregeln

Kommutativgesetz (Vertauschungsgesetz) der Addition: $a + b = b + a$
Bei der Addition darf man die Summanden beliebig vertauschen.
Beispiel: 5 + 8 = 8 + 5 = 13

Kommutativgesetz der Multiplikation: $a * b = b * a$
Bei der Multiplikation darf man die Faktoren beliebig vertauschen.
Beispiel: $9 * 11 = 11 * 9 = 99$

Assoziativgesetz (Verbindungsgesetz) der Addition: $a + b + c = a + (b + c) = (a + b) + c$
Bei der Addition darf man beliebig Teilsummen bilden.
Beispiel: 2 + 8 + 7 = 2 + (8 + 7) = (2 + 8) + 7 = 17

Assoziativgesetz der Multiplikation: $a * b * c = a * (b * c) = (a * b) * c$
Bei der Multiplikation darf man beliebig Teilprodukte bilden.
Beispiel: $3 * 4 * 2 = 3 * (4 * 2) = (3 * 4) * 2 = 24$

Distributivgesetz (Verteilungsgesetz) der Multiplikation: $a * (b + c) = a * b + a * c$ bzw. $a * (b - c) = a * b - a * c$
Bei der Addition und Subtraktion kann entweder die Klammer zuerst berechnet werden, und dann die Multiplikation, oder die Multiplikation wird "aufgeteilt".
Beispiel: $5 * (9 + 12) = 5 * 21 = 105$    ODER    $5 * 9 + 5 * 12 = 45 + 60 = 105$

Distributivgesetz der Division: $(a + b) : c = a : c + b : c$ bzw. $(a - b) : c = a : c - b : c; c != 0$
Bei der Addition und Subtraktion kann entweder die Klammer zuerst berechnet werden, und dann die Division, oder die Division wird "aufgeteilt".
Beispiel: (27 + 9) : 3 = 36 : 3 = 12    ODER    27 : 3 + 9 : 3 = 9 + 3 = 12

Klammernregel: Was in der Klammer steht MUSS zuerst berechnet werden.

Vorrangregeln: POTENZIEREN - PUNKTRECHNUNG - STRICHRECHNUNG

Teilbarkeitsregeln

Eine Zahl ist durch 2 teilbar, wenn die Einerstelle eine gerade Ziffer, also 0, 2, 4, 6 oder 8 ist.

Eine Zahl ist durch 3 teilbar, wenn die Ziffernsumme durch 3 teilbar ist.

Eine Zahl ist durch 4 teilbar, wenn die Zahl, die aus Zehner- und Einerstelle gebildet wird, durch 4 teilbar ist bzw. wenn die Zahl eine Hunderterzahl ist.

Eine Zahl ist durch 5 teilbar, wenn die Einerstelle 0 oder 5 ist.

Eine Zahl ist durch 6 teilbar, wenn sie durch 2 und durch 3 teilbar ist.

Eine Zahl ist durch 8 teilbar, wenn die Zahl, die aus Hunderter-, Zehner- und Einerstelle gebildet wird durch 8 teilbar ist bzw. wenn die Zahl eine Tausenderzahl ist.

Eine Zahl ist durch 9 teilbar, wenn die Ziffernsumme durch 9 teilbar ist.

Eine Zahl ist durch 10 teilbar, wenn die Einerstelle 0 ist.

Rechnen mit Brüchen

echte Brüche: Zähler ist kleiner als der Nenner

unechte Brüche: Zähler ist gleich oder größer als der Nenner

uneigentliche Brüche: Zähler ist ein Vielfaches des Nenners, können als Ganze geschrieben werden

Addition gleichnamiger Brüche: $a/c + b/c = (a+b)/c; c!= 0$
Gleichnamige Brüche werden addiert, indem man die Zähler addiert, und den Nenner unverändert lässt.
Beispiel:$5/8 + 7/8 = (5+7)/8 = 12/8 = 3/2 = 1 1/2$

Addition ungleichnamiger Brüche: $a/b + c/d = (a*d+c*b)/(b*d); b,d != 0$
Ungleichnamige Brüche werden addiert, indem man sie zuerst auf gleichen Nenner bringt, und dann wie gleichnamige Brüche addiert.
Beispiel:$2/8 + 5/3 = (2*3 + 5*8)/(8*3)=(6+40)/24 = 46/24 = 23/12 = 1 11/12$

Subtraktion gleichnamiger Brüche:$a/c - b/c = (a-b)/c; c!= 0$
Gleichnamige Brüche werden subtrahiert, indem man die Zähler subtrahiert, und den Nenner unverändert lässt.

Subtraktion ungleichnamiger Brüche:$a/b - c/d = (a*d-c*b)/(b*d); b,d != 0$
Ungleichnamige Brüche werden subtrahiert, indem man sie zuerst auf gleichen Nenner bringt, und dann wie gleichnamige Brüche subtrahiert.

Multiplikation von Brüchen:$a/b * c/d = (a*c)/(b*d); b,d != 0;$
Zuerst die Brüche in unechte Brüche verwandeln! Brüche werden multipliziert, indem man die beiden Zähler multipliziert und die beiden Nenner multipliziert. Vor dem Multiplizieren, sollte man KÜRZEN!
Beispiel:

Division von Brüchen:$a/b : c/d = a/b * d/c = (a*d)/(b*c); b,c,d != 0$
Zuerst die Brüche in unechte Brüche verwandeln! Brüche werden dividiert, indem man mit dem Kehrwert (Zähler und Nenner vertauschen) des 2. Bruches multipliziert. Vor dem Multiplizieren sollte man KÜRZEN!
Beispiel: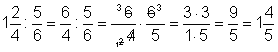

Doppelbrüche:$(a/b)/(c/d) =a/b : c/d= a/b * d/c = (a*d)/(b*c); b,c,d != 0$
Doppelbrüche werden dividiert, indem man den Bruch entweder als Division schreibt, oder die beiden Außenglieder multipliziert und die beiden Innenglieder multipliziert.

Erweitern von Brüchen:$a/b = (a*n)/(b*n); b,n!=0$
Erweitern bedeutet, Zähler und Nenner mit derselben Zahl (ungleich 0) zu multiplizieren. Der Wert des Bruchs ändert sich dabei nicht!

Kürzen von Brüchen:$a/b = (a:n)/(b:n); b,n!=0$
Kürzen bedeutet, Zähler und Nenner durch dieselbe Zahl (ungleich 0) zu dividieren. Die Zahl muss Teiler von Zähler und Nenner sein. Der Wert des Bruchs ändert sich dabei nicht!

Terme

Monome: eingliedrige Terme, z.B. $10x$
Binome: zweigliedrige Terme, z.B. $10x + 7y$
Trinome: dreigliedrige Terme, z.B. $10x + 7y - 8z^2$
Polynome: mehrgliedrige Terme

Addition und Subtraktion: Man kann nur GLEICHE Variablen addieren bzw. subtrahieren. Dabei werden die Koeffizienten (Zahlen) vor den Variablen addiert bzw. subtrahiert.

Klammern: $a + (b + c) = a + b + c$   bzw.   $a + (b - c) = a + b - c$    UND    $a - (b + c) = a - b - c$   bzw.   $a - (b - c) = a - b + c$
Steht vor einer Klammer ein PLUS, so kann die Klammer einfach weggelassen werden.
Steht vor einer Klammer ein MINUS, so muss man beim Weglassen der Klammer die Vorzeichen und Rechenzeichen innerhalb der Klammer ändern.

Multiplizieren mit Monomen: Jedes Glied in der Klammer, wird mit dem Monom multipliziert.
Beispiel: $7x * (4x - 8y + 9) = 28x^2 - 56xy + 63x$

Multiplizieren mit Polynomen: Jedes Glied der ersten Klammer wird mit jedem Glied der zweiten Klammer multipliziert. Achte auf die Vor- bzw. Rechenzeichen!
Beispiel: $(7x+3y)*(4x-8y+9)=28x^2-56xy+63x+12xy-24y^2+27y=28x^2-44xy+63x-24y^2+27y$

Binomische Formeln:

Potenzen

Bezeichnungen: $a^r$: a = Basis, r = Exponent (Hochzahl)

Potenzieren negativer Zahlen: $(-a)^n = +a$, wenn n gerade und $-a$, wenn n ungerade

Multiplizieren: $a^r * a^s = a^(r + s)$
Potenzen mit gleicher Basis werden multipliziert, indem man die Exponenten addiert.
Beispiel: $x^5 * x^8 = x^13$

Dividieren: $a^r : a^s = a^(r - s)$
Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert.
Beispiel: $x^10 : x^8 = x^2$

Potenzieren: $(a^r)^s = a^(r*s)$
Potenzen werden potenziert, indem man die Exponenten multipliziert.
Beispiel: $(x^5)^3 = x^15$

Potenzieren eines Produkts: $(a*b)^r = a^r * b^r$
Ein Produkt wird potenziert, indem JEDER der Faktoren potenziert wird.
Beispiel: $(x * y)^3 = x^3 * y^3

Potenzieren eines Quotienten: $(a/b)^r = (a^r)/(b^r)$
Ein Quotient wird potenziert, indem Zähler UND Nenner poteniert werden.

Wurzeln

Bezeichnungen:$sqrtx$: x = Radikand

Die Addition und Subtraktion unter einer Wurzel kann NICHT auf mehrere Wurzeln aufgeteilt werden:
$sqrt(x+y) != sqrtx + sqrty$    UND    $sqrt(x-y) != sqrtx - sqrty$

Die Multiplikation und Division unter einer Wurzel kann auf mehrere Wurzeln aufgeteilt werden:
$sqrt(x * y) = sqrtx * sqrty$    UND   

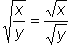
Prozentrechnung - Zinsrechnung

Prozentrechnung

1 Prozent = 1 % = $1/100$ eines Ganzen

1 Promille = 1 ‰ = $1/1000$ eines Ganzen

Bezeichnungen: A = Prozent (Promille)anteil, G = Grundwert p = Prozent (Promille)satz

Berechnen des Prozent (Promille)anteils: $A=G*p/100$    bzw.    $A=G*p/1000$

Berechnen des Grundwerts: $G = A : p/100 = (A*100)/p$    bzw.    $G = A : p/1000 = (A*1000)/p$

Berechnen des Prozent (Promille)satzes: $p=A*100/G$    bzw.    $p=A*1000/G$

Zinsrechnung

Bezeichnungen:

Berechnen der Jahreszinsen: $Z=K_0*p/100$    bzw.    $Z_(eff)=K_0*p_(eff)/100$

Berechnen der Monatszinsen: $Z=K_0*p/100*m/12$    bzw.    $Z_(eff)=K_0*p_(eff)/100*m/12$

Berechnen der Tageszinsen: $Z=K_0*p/100*t/360$    bzw.    $Z_(eff)=K_0*p_(eff)/100*t/360$

Kapital nach n Jahren: $K_n=K_0*(1+p_(eff)/100)^n$

Proportionen

$a : b = c : d$, wobei a und d die Außenglieder sind und b und c die Innenglieder.

Auflösen einer Proportion: $a * d = b * c$
Man multipliziert die beiden Innenglieder und die beiden Außenglieder.

Eine Proportion bleibt richtig, wenn man

  1. die beiden Innenglieder vertauscht: $a : b = c : d iff a : c = b : d$
  2. die beiden Außenglieder vertauscht: $a : b = c : d iff d : b = c : a$

Direkte Proportion: $k = y / x$
Eine Größe y ist direkt proportional zu einer Größe x, wenn der Quotient konstant k ist. k ist der Proportionalitätsfaktor. Grafisch ergibt sich eine Gerade.

Indirekte Proportion: $k = x * y$
Eine Größe y ist indirekt proportional zu einer Größe y, wenn das Produkt konstant k ist. Grafisch ergibt sich eine Kurve.

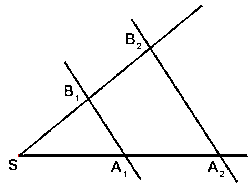
Strahlensatz:
$bar(SA_1) : bar(SA_2) = bar(SB_1) : bar(SB_2)$
$bar(SA_1) : bar(A_1A_2) = bar(SB_1) : bar(B_1B_2)$
$bar(A_1B_1) : bar(A_2B_2) = bar(SA_1) : bar(SA_2)$
$bar(A_1B_1) : bar(A_2B_2) = bar(SB_1) : bar(SB_2)$


Statistik und Wahrscheinlichkeitskeitsrechnung

Statistik

Bezeichnungen:

Arithmetisches Mittel: $barx=(x_1+x_2+cdots+x_n)/n$

Gewogenes Mittel: $barx=(x_1*h_1+x_2*h_2+cdots+x_n*h_n)/n$

Gewichtetes Mittel: $barx=x_1*r_1+x_2*r_2+cdots+x_n*r_n$

Modalwert m: der Wert, der in einer Liste am häufigsten vorkommt

Zentralwert z: der Wert, der in einer geordneten Liste genau in der Mitte steht (gerade Anzahl von Werten) oder der Mittelwert der beiden in der Mitte stehenden Werte (ungerade Anzahl von Werten)

Spannweite R: Unterschied zwischen dem größten und kleinstem Wert einer Liste = $x_(max) - x_(min)$

Quartile q: der Zentralwert teilt eine geordnete Liste in 2 Teile; ermittelt man vom unteren Teil und vom oberen Teil ebenfalls den Zentralwert, hat man die Quartile $q_1$ (unterer Teil), $q_2 = z$ und $q_3$ (oberer Teil) gefunden.

Halbweite w: Unterschied zw. der Quartile $q_1$ und der Quartile $q_3$

Mittlere absolute Abweichung: $d_z=(|x_1-z|+|x_2-z|+cdots+|x_n-z|)/n$

Standardabweichung:$s=sqrt(((x_1-barx)^2+(x_2-barx)^2+cdots+(x_n-barx)^2)/n)$

Winkel

Winkelarten
Spitzer Winkel: zwischen 0° und 90°, 0° < α < 90° BILD
Rechter Winkel: genau 90° BILD
Stumpfer Winkel: zwischen 90° und 180°; 90° < α < 180° BILD
Gestreckter Winkel: genau 180° BILD
Erhabener Winkel: zwischen 180° und 360°; 180° < α < 360° BILD
Voller Winkel: genau 360° BILD

Einheit: 1 Grad = 1° = $1/90$ eines rechten Winkels
Winkelminuten: 1° = 60 '
Winkelsekunde: 1' = 60 ''

supplementär: Zwei Winkel sind supplementär, wenn sie einander auf 180° ergänzen.

komplementär: Zwei Winkel sind komplementär, wenn sie einander auf 90° ergänzen.

Parallelwinkel: Winkel, deren Schenkel paarweise parallel sind, heißen Parallelwinkel. BILD

Normalwinkel: Winkel, deren Schenkel paarweise aufeinander normal stehen, heißen Normalwinkel. BILD

Dreiecke

Allgemein

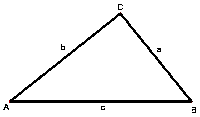
Einteilung nach Seiten:

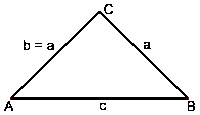
Ungleichseitiges Dreieck Gleichschenkeliges Dreieck Gleichseitiges Dreieck
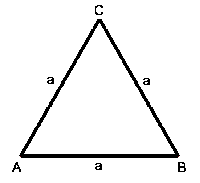Alle 3 Seiten sind unterschiedlich lang. Die Schenkel a und b sind gleich lang. Alle 3 Seiten sind gleich lang.

Einteilung nach Winkeln:

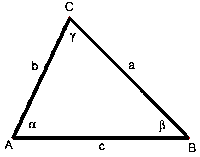
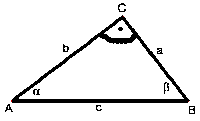
Spitzwinkeliges Dreieck Rechtwinkeliges Dreieck Stumpfwinkeliges Dreieck
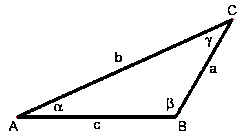Alle 3 Winkel sind spitze Winkel. Ein Winkel ist ein rechter Winkel. Ein Winkel ist ein stumpfer Winkel.
Winkelsumme im Dreieck: 180°

Höhenschnittpunkt H:
ist der Schnittpunkt der Höhenlinien. Diese stehen normal auf die Seite und gehen durch den gegenüberliegenden Eckpunkt. BILD

Schwerpunkt S:
ist der Schnittpunkt der Schwerelinien. Diese gehen von der Mitte der Strecke zum gegenüberliegenden Eckpunkt. BILD

Umkreismittelpunkt U:
ist der Schnittpunkt der Strecken- (Seiten-)symmetralen. Diese gehen durch den Mittelpunkt der Strecke (Seite) und stehen auf diese normal. Der Umkreisradius r geht vom Umkreismittelpunkt zu einem der Eckpunkte. BILD

Inkreismittelpunkt I:
ist der Schnittpunkt der Winkelsymmetralen. Diese halbieren den Winkel. Der Inkreisradius ρ steht normal auf eine Seite und geht zum Inkreismittelpunkt. BILD

EULER'sche Gerade:
Der Höhenschnittpunkt, Umkreismittelpunkt und Schwerpunkt liegen auf einer Geraden, der EULER'schen Geraden. BILD

Umfang: $u = a + b + c$

Flächeninhalt: $A=(a*h_a)/2=(b*h_b)/2=(c*h_c)/2

Das gleichschenkelige Dreieck

Eigenschaften:

Umfang: $u = 2 * a + c$

Pythagoras: $a^2=h_c^2+(c/2)^2$

Das gleichseitige Dreieck

Eigenschaften:

Umfang: $u = 3 * a$

Höhe: $h=a/2*sqrt3$

Umkreisradius: $r=(2*h)/3=(a*sqrt3)/3$

Inkreisradius: $rho=h/3=(a*sqrt3)/6$

Flächeninhalt: $A=(a^2*sqrt3)/4$

Das rechtwinkelige Dreieck

Eigenschaften:

Satz von Thales: Jeder Winkel im Halbkreis ist ein rechter Winkel. BILD

Flächeninhalt: $A=(a*b)/2$

Umkreisradius: $r=c/2$

Inkreisradius: $rho=(a*b)/u$

Satz von Pythagoras: $a^2+b^2=c^2$

Kathetensätze: $a^2=c*p$ (p der rechte Hypothenusenabschnitt) UND $b^2 = c *q$ (q der linke Hypothenusenabschnitt)

Höhensatz: $h^2=p*q$

Vierecke

Das Rechteck

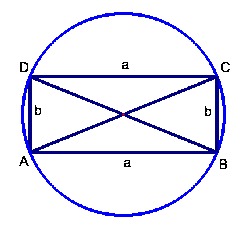
Eigenschaften:

Umfang: $u = 2 * a + 2 * b = 2 * (a + b)$

Flächeninhalt: $A = a * b$

Umkreisradius: $r = d / 2$

Pythagoras: $d^2 = a^2 + b^2$

Das Quadrat

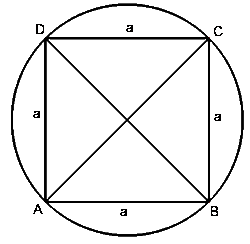
Eigenschaften:

Umfang: $u = 4 * a$

Flächeninhalt: $A = a * a = a^2 = d^2/2$

Umkreisradius: $r = d / 2$

Inkreisradius: $rho = a / 2$

Pythagoras: $d^2 = a^2 + a^2 = a*sqrt2$

Das Parallelogramm

Eigenschaften:

Umfang: $u = 2 * a + 2 * b = 2 * (a + b)$

Flächeninhalt: $A = a * h_a = b * h_b$

Pythagoras: $b^2 = x^2 + h_a^2$
$e^2 = (a + x)^2 + h_a^2$
$f^2 = (a - x)^2 + h_a^2$

Die Raute (der Rhombus)

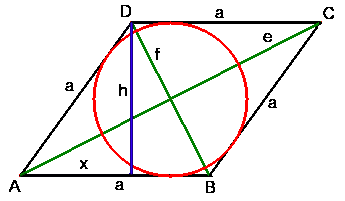
Eigenschaften:

Umfang: $u = 4 * a$

Flächeninhalt: $A = a * h = (e*f)/2$

Pythagoras: $a^2=(e/2)^2+(f/2)^2$
$a^2 = x^2 + h^2$

Das Trapez

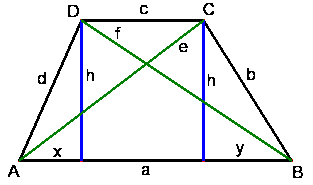
Eigenschaften:

Umfang: $u = a + b + c + d$

Flächeninhalt: $A=((a+c)*h)/2$

Pythagoras: $d^2 = x^2 + h^2$
$b^2 = y^2 + h^2$
$e^2 = (a - y)^2 + h^2$
$f^2 = (a - x)^2 + h^2$

Das gleichschenkelige Trapez

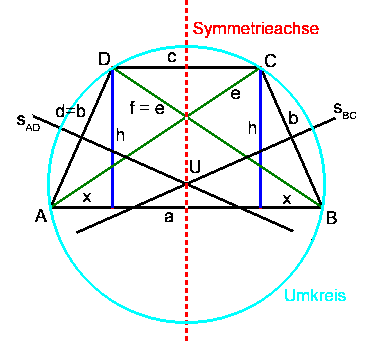
Eigenschaften:

Umfang: $u = a + 2 * b + c$

Pythagoras: $d^2 = b^2 = x^2 + h^2$
$e^2 = f^2 = (a - x)^2 + h^2$

Das Deltoid

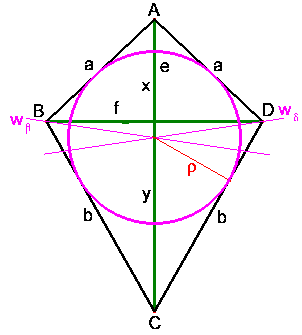
Eigenschaften:

Umfang: $u = 2 * a + 2 * b = 2 * (a + b)$

Flächeninhalt: $A=(e*f)/2$

Pythagoras: $a^2=x^2+(f/2)^2$
$b^2=y^2+(f/2)^2$
$e = x + y$

Allgemeine Vierecke

Kreis

Bezeichnungen:
M ... Mittelpunkt
r ... Radius
d ... Durchmesser = 2 Mal Radius
k ... Kreislinie (Kreis)

Ein Kreis ist die Menge aller Punkte X, die vom Mittelpunkt M denselben Abstand r haben.
$k={X|bar(XM)=r}$

Ein Kreissegment (Kreisabschnitt) ist jene Fläche, die durch den Kreisbogen b und die Kreissehne s begrenzt wird. BILD

Ein Kreissektor (Kreisausschnitt) ist jene Fläche, die durch den Kreisbogen b und 2 Radien begrenzt wird. BILD

Umfang: $u = 2 * r * pi = d * pi$

Flächeninhalt: $A = r^2 * pi = d^2/4 * pi$

Länge des Kreisbogens: $b=(r * pi * alpha)/(180°)$, wobei α der Zentriwinkel des Kreissektors ist

Umfang des Kreissektors: $u = 2 * r + b$

Flächeninhalt des Kreissektors: $A=(r^2*pi*alpha)/(360°)=(b*r)/2$

Umfang des Kreisrings: $u=2*pi*(r_1+r_2)$, wobei $r_1$ der äußere Radius ist und $r_2$ der innere Radius

Flächeninhalt des Kreisrings: $A=(r_1^2-r_2^2)*pi$

Prisma

Bezeichnungen: G = Grundfläche, M = Mantel

Für jedes Prisma gilt:

Der Quader

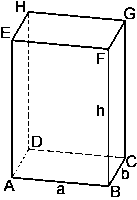
Jeder Quader hat 8 Ecken und 12 Kanten. Je 4 Kanten sind gleich lang. Er hat 6 Begrenzungsflächen, wobei je 2 kongruent (deckungsgleich) sind.

Oberfläche: $O = 2 * a * b + 2 * a * h + 2 * b * h = 2 * (a * b + a * h + b * h)$
Volumen: $V = a * b * h$

Pythagoras: Flächendiagonale (Grundfläche): $d_1^2 = a^2 + b^2$
Flächendiagonale (Seitenfläche): $d_2^2 = a^2 + h^2$
Flächendiagonale (Seitenfläche): $d_3^2 = b^2 + h^2$
Raumdiagonale: $d^2 = a^2 + b^2 + h^2$

Der Würfel

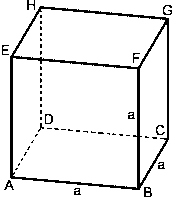
Jeder Würfel hat 8 Ecken und 12 Kanten, wobei alle Kanten gleich lang sind. Er hat 6 gleich große Begrenzungslfächen.

Oberfläche: $O = 6 * a * a = 6 * a^2$
Volumen: $V = a * a * a = a^3$

Pythagoras: Flächendiagonale: $d_1^2 = a^2 + a^2$,    $d_1=a*sqrt2$
Raumdiagonale: $d^2 = a^2 + a^2 + a^2$,    $d=a*sqrt3$




Pyramide

Bezeichnungen: G = Grundfläche, M = Mantel

Für jede Pyramide gilt:

Regelmäßige quadratische Pyramide

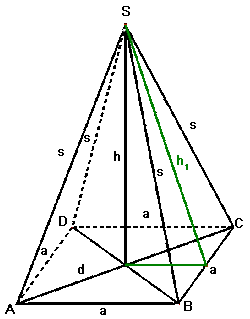
Grundfläche: Quadrat, Mantel: 4 gleichschenkelige Dreiecke

Oberfläche: $O = a^2 + 2 * a * h_1$

Volumen: $V=(a^2*h)/3$

Pythagoras: $s^2=h^2+(d/2)^2$
$s^2=h^2+a^2/2$
$s^2=h_1^2+(a/2)^2$
$h_1^2=h^2+(a/2)^2$

Regelmäßige sechsseitige Pyramide

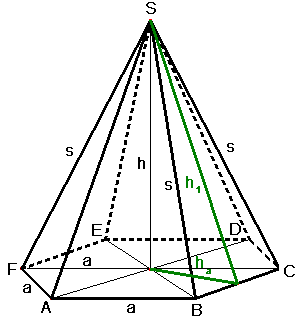
Grundfläche: Sechseck (6 gleichseitige Dreiecke), Mantel: 6 gleichschenkelige Dreiecke

Oberfläche: $O=(3*a^2*sqrt3)/2+3*a*h_1=3*a*((a*sqrt3)/2+h_1)$

Volumen: $V=((3*a^2*sqrt3)/2*h)/3 = (a^2*h*sqrt3)/2$

Pythagoras: $s^2 = a^2 + h^2$
$h_a=a/2*sqrt3$
$h_1^2=(3a^2)/4+h^2$
$s^2=h_1^2+(a/2)^2$

Regelmäßiges Oktaeder

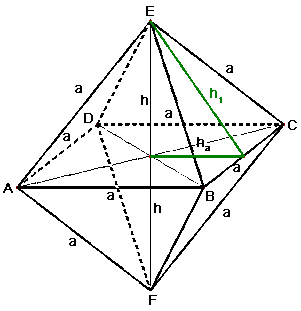
Ein regelmäßiges Oktaeder ist eine quadratische Doppelpyramide, wobei alle Seiten gleich lang sind. Die Oberfläche besteht aus 8 gleichseitigen Dreiecken, das Volumen entspricht dem doppelten einer regelmäßigen quadratischen Pyramide, wobei zu beachten gilt, dass die Höhe durch a ausgedrückt werden kann.

Oberfläche: $O = 2 * a^2 * sqrt3$

Volumen: $V=(a^3*sqrt2)/3$

Pythagoras: $h_a=a/2*sqrt3$
$a^2 = 2 * h^2$
$h_1=(a*sqrt5)/2$

Regelmäßiges Tetraeder

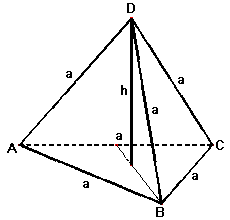
Ein regelmäßiges Tetraeder ist eine regelmäßige dreiseitige Pyramide, wobei alle Seiten gleich lang sind. Die Oberfläche besteht aus 4 gleichseitigen Dreiecken.

Körperhöhe: $h=(a*sqrt6)/3$

Oberfläche: $O = a^2 *sqrt3$

Volumen: $V=(a^3*sqrt2)/12$



Zylinder - Kegel - Kugel

Der Drehzylinder

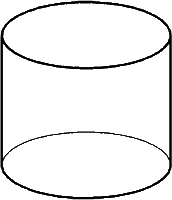
Mantelfläche: $M = 2 * r * pi * h$

Oberfläche: $O = 2 * r * pi * (r + h)$

Volumen: $V = r^2 * pi * h$

Gleichseitiger Drehzylinder: Durchmesser = Höhe

Mantelfläche: $M = 4 * r^2 * pi$

Oberfläche: $O = 6 * r^2 * pi$

Volumen: $V = 2 * r^3 * pi$

Der Drehkegel

Mantelfläche: $M = r * pi * s$

Oberfläche: $O = r * pi * (r + s)$

Volumen: $V=(r^2*pi*h)/3$

Pythagoras: $s^2 = r^2 + h^2$

Gleichseitiger Drehkegel: Durchmesser = Seitenkante

Mantelfläche: $M = 2 * r^2 * pi$

Oberfläche: $O = 3 * r^2 * pi$

Volumen: $V=(r^3*pi*sqrt3)/3$

Die Kugel

Oberfläche: $O = 4 * r^2 * pi$

Volumen: $V=(4*r^3*pi)/3$